En líneas generales, el término dificultades matemáticas se refiere a los niños cuyo pobre logro en matemáticas es causado por una variedad de factores, desde la instrucción deficiente a los factores ambientales, y representa una construcción más amplia que el término discapacidad matemática o discalculia. Los niños con dificultades matemáticas tienen un desempeño promedio bajo, o un desempeño pobre en matemáticas, pero no todos los niños con dificultades matemáticas tendrán discalculia, que se cree que se debe a una debilidad inherente en la cognición matemática no atribuible a causas socioculturales o ambientales (Mazzoco, 2007).  

La discalculia, que es muy probable que no sea el nombre más acertado, es una dificultad del aprendizaje de las matemáticas la cual, a pesar de tener una alta prevalencia y considerables repercusiones escolares, sociales y laborales, ha suscitado un menor interés con respecto a la escritura y, sobre todo, la lectura. Mientras que la lectura es un proceso unitario, las matemáticas abarcan habilidades muy heterogéneas. No es lo mismo, por ejemplo, el aprendizaje memorístico de las tablas de multiplicar, que el cálculo mental. Pero es que, además, dentro de una misma operación matemática están implicadas habilidades y funciones cognitivas distintas, como la memoria semántica, la memoria de trabajo, la atención, la cognición espacial, velocidad de procesamiento, las habilidades perceptivas, el razonamiento o el sentido numérico.

Los criterios de diagnóstico, continuamente cambiantes, y las definiciones variables entre los ámbitos educativo y sanitario añaden un factor de confusión adicional entre los dos términos. Los términos como discalculia y logros matemáticos deficientes se suman a la confusión, ya que no está claro si los términos están destinados a ser sinónimos o superpuestos (Mazzoco, 2005). Como dice Artigas-Pallarés (2011), cabe plantearse si las diversas denominaciones equivalentes a discalculia significan los mismo. Así, podemos ver denominaciones como discapacidades matemáticas, dificultades matemáticas, discapacidades del aprendizaje matemático, discalculia del desarrollo, síndrome de Gerstmann del desarrollo,… 

Como definición genérica de la discalculia, Kosc (1974), propone la siguiente:

<<Trastorno estructural de las capacidades matemáticas que tiene su origen en un trastorno biológico, genético o adquirido, de aquellas partes del cerebro que son el sustrato anatomofisiológico de la maduración de las capacidades matemáticas, sin trastorno de las funciones mentales generales>>.

Por tanto, consideraremos la discalculia como secundaria a déficits en procesos cognitivos, lo cual se confirma en algunos casos de forma clara, como la cognición espacial, y en otros existen contradicciones, como ocurre con la memoria de trabajo (Castro-Cañizares, Estévez-Pérez y Reigosa-Crespo, 2009). Nosotros creemos que las dificultades en el procesamiento matemático están causadas por dichos déficits primarios. 

Por su parte, las principales clasificaciones internacionales hablan, por un lado, de Trastorno Específico del Cálculo (CIE), dentro de los Trastornos específicos del desarrollo del aprendizaje escolar (F81), definiéndolo como un impedimento específico en las habilidades aritméticas, no sólo explicable sobre la base del retraso mental general o de la escolaridad inadecuada, que implica el dominio de habilidades computacionales básicas en lugar de habilidades matemáticas más abstractas (WHO, 1992). Por otro lado, el DSM-5, como un tipo específico de una categoría única de Trastornos de Aprendizaje, estableciendo que las dificultades deberían haber persistido durante al menos seis meses a pesar de las intervenciones, y las habilidades deberían ser sustancialmente inferiores a las esperadas para la edad. Los déficits deben interferir con el funcionamiento, como lo confirman las medidas estandarizadas de rendimiento administradas individualmente y la evaluación clínica integral. Incluye posibles déficits en el sentido numérico, la memorización de los hechos matemáticos, el cálculo y el razonamiento matemático (APA, 2013). 

Debido a esto, existen diferentes propuestas en la conceptualización de lo que llamamos, vuelvo a repetir que muy posiblemente de forma equivocada, discalculia, pasando de posiciones que conciben la discalculia como un trastorno unitario, a otros modelos que proponen subtipos de dificultades del aprendizaje matemático. Otros autores incluso, con buena parte de razón, y como ya hemos mencionado en entradas anteriores, consideran que no se puede hablar de dislexia, disortografía, discalculia,…, o de trastornos del aprendizaje, ya que, según ellos, no puede trastornarse aquello con los que no se parte de nacimiento. En caso de ser así, tendría que existir un trastorno para cada una de las creaciones humanas como, por ejemplo, trastorno digital para los incapaces de utilizar un aparato tecnológico, o del conducir, para los que no aprueban el carnet de conducir por mucho que se empeñen. 

Así, más allá de la concepción de la discalculia como disfunción del “circuito del cálculo”, existen otras propuestas teóricas que, resumidamente, sugieren las siguientes formas de entender y clasificar la discalculia (Artigas-Pallarés, 2011):

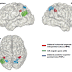
En relación a la segunda propuesta, muchos investigadores han intentado describir subtipos de dificultades en el aprendizaje de las matemáticas (Geary, 1990; Rourke, 1993; Fuchs y Fuchs, 2002; Jordan et al., 2003; Geary, 2004; Geary y Hoard, 2005). Geary fue uno de los primeros que intentó conectar el "Trastorno de las Matemáticas" con los déficits neuropsicológicos (Geary, 1994). Él postuló tres subtipos de déficits (Geary y Hoard, 2005):

Sin embargo, tales clasificaciones no son completamente satisfactorias porque, en general, los perfiles de los niños encontrados en la práctica no parecen pertenecer a ningún subtipo, sino que están constituidos por varias características pertenecientes a diferentes subtipos (Desoete, 2007). 

Las psicólogas Blakemore y Frith (2011) afirman que no existe demasiado sentido buscar una región cerebral que haga matemáticas, debido a que hay diferentes aspectos que componen las matemáticas y que implican diferentes regiones. El procesamiento matemático y el cálculo son capacidades complejas, que implican la participación de diferentes capacidades cognitivas (verbales, atencionales, espaciales, memorísticas y ejecutivas), por lo que su sustrato cerebral se encuentra distribuido en diferentes áreas y/o regiones tanto corticales como subcorticales, conectadas entre sí formando redes neuronales complejas. Esto conlleva que puedan surgir dificultades de diversa índole en el procesamiento numérico (Serra, 2013). La interconexión y múltiples factores del cálculo también conllevan que la alteración en uno de los componentes cognitivos que operan en el cálculo, por ejemplo, el lenguaje en el hemisferio izquierdo, puede llevar a que se vean afectadas la compresión y producción de números. Esto refleja que existen diferentes sistemas cerebrales implicados en los distintos aspectos de los números, que se integran para dar coherencia y sentido como un todo. Lo que sí podemos afirmar es que aún no tenemos el suficiente conocimiento del funcionamiento de nuestro cerebro matemático. Hasta el momento, los estudios parecen indicar que diferentes regiones parietales y prefrontales contribuyen de manera significativa a la función numérica (Serra-Grabulosa et al., 2010). 

El matemático y doctor en psicología cognitiva Stanislas Dehaene (Cohen y Dehaene, 1994, 1996; Dehaene, 1992, 1997, 2007; Dehaene y Cohen, 1991, 1995, 1997, 2007, 2016; Dehaene y Mehler, 1992;) es, sin duda, junto con su equipo, el investigador que ha dado un mayor impulso al estudio de las bases neurocognitivas de las matemáticas desde finales de los ochenta, tanto mediante el estudio de pacientes lesionados, como con las modernas técnicas de neuroimagen. En estos y otros estudios, se asocia el área inferior del lóbulo parietal como la base del cerebro matemático, ya que esta región se activa durante cualquier actividad numérica (Cantlon et al., 2006). Las lesiones en esta región pueden dejar al paciente totalmente incapaz de ejecutar incluso cálculos tan sencillos como 3-1 o 7x8 (Warrington, 1982; Takayama, Sugishita, Akiguchi, Kimura, 1994; Dehaene y Cohen, 1997). Butterworth (1999) afirma que "está claro que nuestro Cerebro Matemático está localizado en el lóbulo parietal izquierdo". Pero el hecho de que la región parietal inferior parezca jugar un papel crucial en el sentido numérico, no quiere decir que sea la única región cerebral implicada en el procesamiento numérico.

Dehaene, Piazza, Pinel y Cohen (2003), identifican el que llaman “circuito del cálculo”, que consta de tres regiones (ver figura):

• Surco intraparietal horizontal superior bilateral (en color rojo en la figura): manipulación de cantidades o sentido numérico (comparación de cantidades numéricas, estimaciones, sustracciones y aproximaciones). Se activa en tareas de cálculo exacto y de cálculo aproximado, de aspectos no simbólicos, como de aspectos simbólicos (Serra, 2013). La activación del surco intraparietal está exclusivamente relacionada con el procesamiento numérico, habiéndose aislado para su comprobación de tareas atencionales, espaciales, del movimiento de los ojos y de los dedos. Se activa con la simple presencia de estímulos numéricos, siempre y cuando estos tengan algún significado cuantitativo, independientemente del formato y tipo del estímulo utilizado, aunque parece ser que existen diferentes grupos de neuronas que responden selectivamente a un formato concreto y otros grupos de neuronas a otro. El surco intraparietal derecho se ocupa de la estimación de magnitudes, mientras el izquierdo de tareas de comparación, tanto de estímulos simbólicos (dígitos) como no simbólicos (ej.: puntos), como de cálculos numéricos. La realización de sumas, restas y multiplicaciones es bilateral, pudiendo verse afectadas si hay lesión en cualquiera de los hemisferios. El surco intraparietal también se encarga de la recuperación de hechos numéricos de la memoria a largo plazo (Serra, 2013). 
• Lóbulo parietal posterosuperior bilateral (en color azul en la figura): esta área, relacionada con tareas espaciales y de memoria de trabajo espacial, se asocia con tareas atencionales durante la resolución del cálculo, como por ejemplo, tareas de comparación numérica, cálculo aproximado, sustracción aproximada, contabilización, etc. (Cohen-Kadosh et al., 2011; Kaufmann et al., 2008; Chochon, Cohen, Van de Moortele y Dehaene, 1999). Esta región es claramente multimodal, ya que también se encarga de tareas visoespaciales y de memoria de trabajo espacial (Serra, 2013). 
• Circunvolución angular izquierda (en color verde en la figura): región clave en los procesos automáticos y dependientes del lenguaje implicado en la realización de problemas aritméticos. Se encarga de la  representación simbólica, mediante palabras o mediante números. Con ello se permite el cálculo exacto (operaciones sencillas exactas que aprendemos de memoria para agilizar el cálculo, como las tablas de multiplicar o las operaciones aritméticas simples con cifras pequeñas menores de 10). Cuando es una multiplicación no automatizada, no interviene el giro angular, sino el surco intraparietal bilateral y áreas prefrontales relacionadas con la atención y la memoria de trabajo. Sustenta la representación cerebral no semántica de las cantidades (procesar el dígito 6 sin asociarlo con una cantidad numérica concreta), (Price y Ansari, 2011; Grabner et al., 2009; Dehaene et al., 1999). Existe una correlación positiva entre la activación del giro angular izquierdo y la competencia matemática (Grabner et al. 2007), al existir mayores automatismos. Por esta razón tiene sentido que a los niños disléxicos les cueste memorizar las tablas de multiplicar, ya que proceso de codificación fonológica depende de la misma región cerebral (Boix et al., 2015). Es el centro de la lesión en el Síndrome de Gerstmann.

A partir de la identificación de estas tres regiones descritas anteriormente, se puede inferir teóricamente la existencia de tres subtipos diferenciados de dificultades en el cálculo:

• Por déficit en el sentido numérico.
• Por alteración en la atención espacial.
• Por dificultades verbales.

Sin embargo, cabe plantearse si en la práctica es posible disociar dichos subtipos dentro de los trastornos del neurodesarrollo del cálculo. De hecho, cualquier déficit en alguno de estos módulos es muy probable que interfiera en el desarrollo en la función de los otros módulos, puesto que se desarrollan de manera muy interrelacionada, lo que impide la aparición de casos puros como ocurre en la acalculia (lesión adquirida) (Artigas-Pallarés, 2011).

Dehaene y Cohen (1995) describen el modelo cognitivo del triple código en el que diferencia tres formatos de representación de las cantidades: el arábigo (5), el verbal (cinco) y un formato abstracto ligado a la magnitud, y que está relacionado con el concepto de numerosidad. Estos autores consideran que el sistema visual (córtex occipito-temporal inferior) del hemisferio izquierdo está asociado con el reconocimiento tanto de cifras arábigas ("7") como de palabras escritas ("siete", mientras que la misma región del hemisferio derecho sólo reconoce las arábigas. En el caso de identificación y producción de palabras habladas, es la región perisilviana del hemisferio izquierdo la que está implicada. Esta región participa también en un circuito cortico-subcortical que comprende también los ganglios basales del hemisferio izquierdo, que se activan en tareas aritméticas rutinarias (tablas de sumar y multiplicar).

Los circuitos dedicados a coordinar las intervenciones de las demás áreas están ubicados posiblemente en el córtex prefrontal, en el córtex cingulado anterior y los circuitos frontosubcorticales, interviniendo en la supervisión de conductas no automatizadas, como son las tareas que requieren planificación, organización, ordenación secuencial, toma de decisiones, corrección de errores, mantenimiento de resultados intermedios y puesta en marcha de la memoria de trabajo. Ante cualquier tarea que requiera resolver un cálculo más complejo se activará esta región cerebral que, al mismo tiempo, realiza una labor de asistencia al giro angular en la recuperación de hechos aritméticos (red frontoparietal) (Jost et al., 2011), identifica y corrige los errores (Menon et al., 2002), y realiza tareas de memoria de trabajo y de focalización de la atención en tareas numéricas. Las regiones prefrontales se activan en mayor medida en los niños pequeños, con menor experiencia y automatización del cálculo, activando mayores recursos atencionales y de meoria de trabajo. Por el contrario, en los niños pequeños se activan en menor medida las regiones parietales. Por tanto, parece que se va dando una especialización parietal. Las áreas prefrontales también se activan más ante operaciones aritméticas incorrectas.

Existen otras regiones cerebrales asociadas al cálculo, como la ínsula anterior izquierda, el cerebelo y el núcleo caudado. Hasta donde se sabe hoy día, la ínsula anterior izquierda y la corteza cerebelosa participan en la recuperación de hechos aritméticos (Zago et al., 2001). La corteza cerebelosa central se asocia con el aprendizaje de secuencias de movimientos realizados con los dedos y con la manipulación de objetos en tres dimensiones (Serra, 2013). Por su parte, el núcleo caudado participa también en el procesamiento numérico y el cálculo, aunque se desconoce con exactitud su función, habiéndose relacionado con cálculos novedosos (no entrenados), y los problemas aritméticos complejos que requieren varios pasos para su resolución (Serra, 2013).

Para cantidades superiores a las posibles de subitizar necesitamos contar. Sin embargo, disponemos de una capacidad de estimación aproximada de cantidades mayores, por ejemplo, para estimar cantidades de 9-10 ítems, o cantidades mucho mayores como los asistentes a un concierto, manifestación, etc. Tendemos a sobreestimar las cantidades pequeñas y a subestimar las cantidades grandes. La estimación es un proceso de mapeo entre la numerosidad exacta y la aproximada, dando una etiqueta a la cantidad de elementos percibidos sin contarlos, lo cual es impreciso. Las estimaciones dependen de factores como la densidad, la regularidad del espacio en la que se distribuyen los elementos y la luminosidad, realizando estimaciones mayores con menor densidad, espacios regulares y menor luminosidad. Los humanos, incluidos los niños preverbales, y algunos animales, como peces, pájaros y primates, poseemos un sistema numérico aproximado. Se han encontrado áreas cerebrales relacionadas con la numerosidad de grandes elementos, como el surco intraparietal lateral y ventral. Existen diferencias individuales, así como a lo largo del desarrollo, habiéndose observado un gran aumento de precisión entre los 11 y 16 años, así como un decrecimiento lento desde los 30 a los 85 años. No existen diferencias significativas entre adultos jóvenes entre 18 y 25 años, y adultos mayores entre 60 y 77 años. Se han encontrado altas correlaciones entre la precisión del ANS con el rendimiento en tareas matemáticas simbólicas. Al igual que el ANS parece ser básico en la habilidad matemática posterior, también se da una relación inversa, en el sentido de que la educación y experiencia matemática incrementa la precisión del ANS. Además, se ha encontrado que el entrenamiento del ANS mejora el rendimiento en matemáticas simbólicas, aunque hay controversias al respecto. Un fenómeno curioso es que tendemos a asociar el espacio izquierdo a números pequeños y el espacio derecho a números grandes, ocurriendo al contrario en población árabe (en la que leen y escriben de derecha a izquierda). Sin embargo, en niños que aún no han sido alfabetizados se da la tendencia de izquierda a derecha.

En la habilidad de contar en voz alta y en las estrategias para contar intervienen el desarrollo del lenguaje y la lectoescritura. Por tanto, una alteración en el desarrollo del lenguaje y de la lectoescritura puede provocar un retraso en la adquisición de la habilidad de contar y en el almacenaje de hechos numéricos y aritméticos (Serra, 2013).

La importancia de la magnitud de los números es determinante en la realización de tareas aritméticas, especialmente en las de cálculo aproximado. Cuando se comparan dos números entre sí, a igual distancia entre ellos, existe mayor dificultad conforme se incrementan sus valores. Es más fácil comparar la distancia entre 4 y 2, que entre 6 y 4. Cuanto menor es la distancia entre dos números, más tiempo se emplea en compararlos. Se tarda más en compara 5 y 6, que 8 y 2.

En todas estas operaciones, la magnitud de los números representados es un aspecto de gran importancia, ya que la manipulación de números grandes afecta a la dificultad del proceso.

La realización de la suma lleva implícito el hecho de entender que hay que unir dos conjuntos de elementos y contar el total de estos. Esto puede conseguirse a través de diferentes estrategias:

Se cuentan los elementos del primer conjunto, y se continua contando con los del segundo conjunto. Por ejemplo, 3+4, se cuenta un, dos tres, y se continua con el segundo conjunto cuatro, cinco, seis y siete. Otra forma es que, pariendo de la cifra del primer conjunto (3), se sigue contando los elementos del segundo conjunto. Una tercera estrategia, más sencilla y con menor riesgo a equivocarse, es partir del conjunto mayor (4), y seguir contando los elementos del conjunto menor. Una estrategias más es saberse de memoria las sumas de pequeñas cantidades, de tal forma que no sea necesario contar. Te las aprendes como si se tratasen de unas tablas hasta automatizarlas (numbers facts retrieval o recuperación de hechos numéricos). El aprendizaje de la resta puede basarse en estrategias similares, aunque resulte algo más complejo para los niños.

Respecto a la multiplicación y la división, han de introducirse más tarde, explicándose bajo la base de que sumas o restas repetidas pueden representarse más fácilmente con estas operaciones. La división da lugar a otros conceptos matemáticos como las fracciones y los porcentajes.

Posteriormente, y en paralelo a hacer más complejas las operaciones aritméticas, se van introduciendo conceptos de magnitud, sistemas de medida, geometría, proporcionalidad, estadística, probabilidad, álgebra, trigonometría, etc. También se van introduciendo los problemas matemáticos, que es una de las áreas de investigación incipientes en la actualidad.

A lo largo de los últimos años, se han propuestos diferentes modelos para explicar el procesamiento numérico, destacando dos por encima de todos ellos: el modelo de McCloskey et al. (1985), y el modelo de triple código de procesamiento de Dehaene et al. (2003).

McCloskey et al. (1985), distinguen tres componentes: el sistema de procesamiento numérico, el sistema de cálculo y el sistema de representaciones semánticas. Las alteraciones en uno u otro sistema se manifiestas de manera diferente. Así, las características de cada sistema serían:

Por su parte, el modelo del triple código (Dehaene y Cohen, 1995; Dehaene et al., 2003), afirma que el procesamiento aritmético depende de tres sistemas con funciones diferentes, organizados en módulos: el módulo verbal, el visual y el de magnitud. Las operaciones que son relativamente simples, que dependen del lenguaje, son procesadas por el sistema verbal (hemisferio izquierdo), mientras que las tareas más complejas, que requieren la estimación de magnitudes y la representación visual se encuentran localizadas en los dos hemisferios, implicando los sistemas visual y de magnitud. En una entrada posterior volvemos a hacer referencia a este modelo.

Los estudios realizados confirman parcialmente ambos modelos. En términos de la representación del significado numérico, hace falta una línea mental analógica, como se propone el modelo del triple código. Con relación  la representación de los procedimientos específicos de cálculo (suma, resta, multiplicación y división), el modelo de McClosky et al., predice que cada uno de ellos puede estar afectado selectivamente por una lesión, hecho que apoyan los datos empíricamente. En cuanto a la controversia acerca de la transcodificación de formas arábigas a verbales, existen datos a favor de la existencia de una vía semántica y de otra asemántica.

Para saber más y mejor: